Journal of Unification Studies Vol. 14, 2013 - Pages 163-182
In the 2007 edition of this journal I wrote an article with the title “The Yin and Yang of Prime Numbers: Finding Evidence of Unification Thought’s Teachings on the Dual Characteristics in Prime Number Reciprocals.”[1] It provided a rather general introduction to my findings in the world of numbers.
Despite some unavoidable overlap with that article, the current focus is solely on the two types of dual characteristics as explained in Rev. Sun Myung Moon’s Unification Thought and Divine Principle and how his insights parallel with my number research findings.
Friends of mine ask me occasionally what the practical applications of my numeric discoveries are, almost like telling me “So what?” While I understand these concerns, there is more to life than just pragmatism. We also benefit in life from human created beauty, such as art, music, poetry, dance, architecture, as well as from divinely created natural beauty like flowers and sunsets. It is my firm conviction when the inherent beauty and structure of numbers is revealed, people’s grasp of and love for math will improve, which is actually of great pragmatic benefit. Consider the fact that 70% of students continue to fail at math, and that “hating math” seems a popular sentiment (sadly, I hear it all the time).
An article on number theory, a branch of mathematics, in a theological journal may seem out of place, and yet we will see that it is not. After all, Moon himself has repeatedly emphasized the importance of numbers, especially during his final earthly years, as he saw them in a spiritual and providential light. It would make for fascinating reading if someone were to thoroughly study Rev. Moon's reading on the significance of numbers.
On my side, I have been simply studying the very nature and characteristics of numbers themselves, from a purely arithmetic-based analytical and intellectual perspective. I therefore assign no particular meaning to any number, like 12, 40, etc. Generally, number theory is not to be confused with numerology.
Two Types of Dual Characteristics
Anyone familiar with Unification Thought knows that Rev. Moon has taken the ancient Oriental philosophical notion of the dual characteristics of yang and yin[2] a step further by making a further delineation, as all yang and yin (e.g. a man and a woman) also each possess another pair of dual characteristics, namely that of internal character (mind/spirit) and external form (body/matter), which in the original Korean of Unification Thought is called sungsang (invisible element) and hyungsang (visible element). What fascinated me was the discovery that these two-fold dual characteristics also apply to the world of numbers!
What follows below is an introductory encapsulation of these findings as they relate to this notion of the two types of dual characteristics, which are explored fully in my book The Secret World of Numbers. In Unification Thought the topics of subject (initiating force) and object (responding effect) between whom giving and receiving action takes place, but these considerations are harder to discern in the world of numbers. I will briefly touch upon this terminology.
Numbers behave in a certain fixed and even predictable way, and their behavior is also absolute. Rev. Moon, who repeatedly stressed the absoluteness of God and Divine Laws, routinely urged scientists who gathered for the International Conferences on the Unity of the Sciences (ICUS) to center their papers on the theme of and quest for absolute values. Certainly, numbers belong to this absolute realm, for 1 + 2 will always be 3. Also, anyone studying the numbers ruling just our solar system will be intrigued by the numbers involved.[3] Scientists continuously marvel over the fact the universe can at all be expressed in mathematical formulas.
Dual Aspects of Whole Numbers
Let’s start at the very beginning
Like our ABC’s, which we learned in elementary school, we have to start with the numbers 0 through 9, especially since all numbers, large and small, make use of these 10 digits.[4] When we count, we start with single-digit numbers, but soon naturally expand to 2-digits (e.g., 21, 28, 35, etc.), and many more digits as we keep counting towards infinity. Thus, the start of the table of 7 looks this: 7-14-21-28-35-42-49-56-63-70-77-84-etc.
Of course, this is elementary math. But to me, the important thing to observe is this: didn’t we in fact start out with a single digit, namely 7, that became two digits in 14, 21, etc.? We normally take this growth of the number of digits for granted, but looking at it from another perspective, we also know that the initial rule of the start of only one single digit has also been broken. Thus, I am taking the first number, a single digit, namely 7, as my guide and starting point. But how can we turn all these double, triple, and many-fold digits into a single digit? Very simply, through the process of adding the digits together until we can no longer do so, which is called reduction. We reduct the digits to a final single digit. Thus 21 becomes 2 + 1 = 3, and 35 becomes 8 (3 + 5), etc.[5]
When we look at the multiplication table of 7 from this new perspective, and it is going to look very different: 7 remains 7; 14 reducts to 5; 21 to 3; 28 to 1; 35 to 8; 42 to 6; 49 to 4; 56 to 2, and 63 reducts to 9, and all the higher numbers reduct to a repeat of this new series, which is: 7-5-3-1-8-6-4-2-9---7-5-3-1-8-6-4-2-9---etc.;
Interestingly, we see odd digits in descending order: 7-5-3-1, followed by even descending digits: 8-6-4-2; with the 9 naturally in the 9th position, as the reduction of any multiple of 9 is always 9.
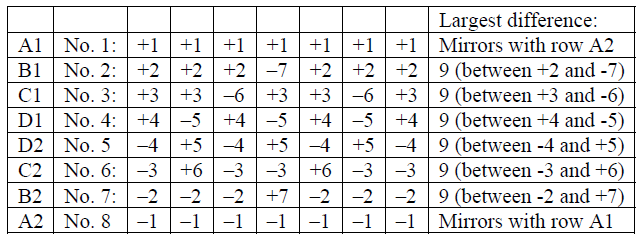
One surprise: 7-5-3-1 when reversed into 1-3-5-7 and then added to the descending order of 8-6-4-2- adds to 9-9-9-9 (of course, I could also have reversed the second group only to achieve the same total; I have two choices, one based on a from-the-left approach; the other a from-the-right approach). Also note that in 7-5-3-1-8-6-4-2, the outermost digits add to 9 (1st and 8th position); the next two digits (2nd and 7th position) add to 9, as well as the 3rd and 6th digits, 3 and 6, and finally the innermost digits 1 and 8 in 4th and 5th position. We shall see more of these types of mirrors. This is our first encounter with a yang-yin type of phenomenon.
Do you see what I have achieved by the process of reduction? From the external visible series created by the multiplication table of any number, I was on a quest to discern the fundamental, invisible, or sungsang element of these numbers. In this case, the invisible sungsang aspect is the reducted form of any multiplication table; and we shall see that with prime number reciprocals, the visible–invisible hyungsang-sungsang aspects are similarly present, but also mirrored/reversed.
The phenomenon of mirrors kept showing itself in my number analysis, and will become more apparent here. Thus, true to Unification Thought, I believe I have found the sungsang and hyungsang of whole number multiplication tables.
Numeric differences
Before I discuss this a bit further, let us first look at numeric differences. We can look our prime example, the series of the number 7, (9)-7-5-3-1-8-6-4-2-9-etc., from a perspective I have not seen applied in number theory, namely that of numeric differences between consecutive digits:

Thus, most interestingly, we have a total of seven -2 subtractions, with a total of -14, and we have a total of two +7 (given in bold) additions, for total of +14. We see a perfect balance of plus and minus values, or what I like to also call a mirror: 7x -2 and as 2x +7. A form of yin and yang? Anyone familiar with Unification Thought will not be surprised here. After all, if Unification Thought is true, it should show itself in all kinds of hitherto unexpected places. So far so good!
These totals balance, or cancel each other out. Is this just a coin¬ci-dence? We shall see that it is not, after we look at the reducted table for all the first nine numbers, which is the foundation for all numbers greater than a single digit (note that the differences in each 3rd row are only between consecutive reductions):
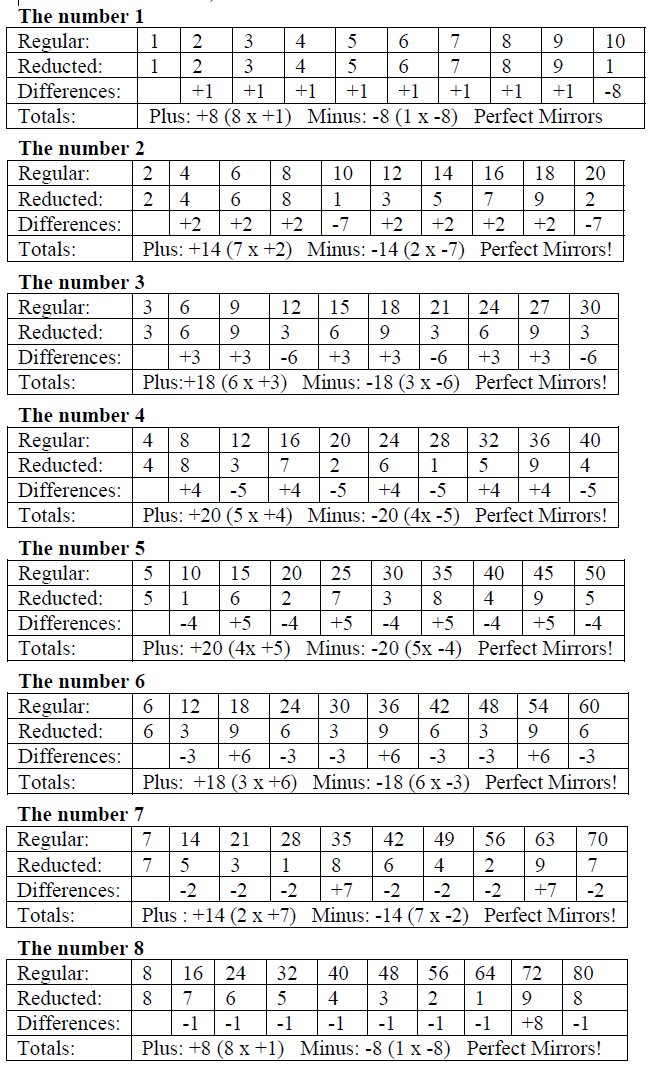
I have omitted the table of 9, as reductions of multiples of 9 are always 9. Let’s now look at the results of the reductions in a more easy to see table:
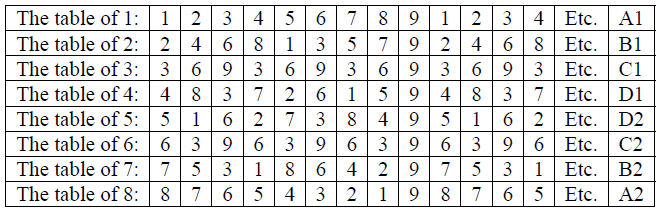
The rows of 1 and 8 (note that 1 + 8 = 9) are mirrors, as they run in opposite directions (A1 and A2). The same is also true for B1 and B2, C1and C2 and D1 and D2. Please take a careful look at this.
Four-directional mirrors
Below I have placed two lines, in the form of an “x,” one from the left bottom corner to the top right corner and the other from the top left corner to the bottom right corner, thus effectively dividing our square of reductions into four triangles. When we compare the numbers in each of these four compartments, we will see again Yang-Yin types of symmetrical mirrors:
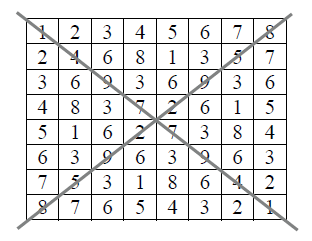
Compare numbers in the top triangle: ▼ with the left triangle: ►, then with the right triangle: ◄, and finally with the bottom triangle: ▲ in order to see the mirror “images” appear. One example is given below, and I invite the reader to discover the others. The left triangle and the top triangle:
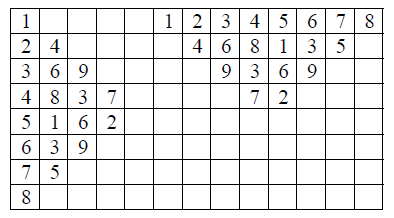
If we interpret these two halves as a type of yin/yang, then the notion of equality between yin and yang in all its forms and levels, as stated in DP/UT, would automatically be confirmed. If you look carefully along a central vertical and horizontal line, you will see even more mirrors.
Also, when the values are read diagonally (along this line: /), we are discovering palindromes, like 1; 2-2; 3-4-3; etc., and when read in mirror image (like so: \), we discover palindromes of 8; 7-7-; 6-5-6; etc. I now invite you to see these and all kinds of other patterns along vertical and diagonal lines, and I have added a checkered pattern to aid you visually:

During especially the past decade of his life, Rev. Moon continually emphasized how from a center (God), we can have six (or double of 3) basic directions, as well as dynamics of relationships, namely: front and back, left and right, as well as top (up) and bottom (down). Such a model is 3-dimensional. In a palindrome table as shown above, we see also left-right as well as up and down dimensions. Even though Rev. Moon's model is 3D,
I hope it is not too farfetched to see parallels in the left-right and up-down dimensions of palindromes and palindrome tables.
In the table below I have indicated the numeric differences in the table of reductions. I have added labels to each row: A1, A2, etc. Again, notice the correlations between A1 and A2 (1 and 8), B1 and B2 (2 and 7), C1 and C2 (3 and 6), and between D1 and D2 (4 and 5) (and we could have added: between 0 and 9). Notice again the centrality of the number 9. Between these pairs we see perfectly mirrored plus and minus values:
Since 1, 10, 19, 28, etc. all reduct to 1, we should also make a table of reductions to 1, to 2, to 3, etc., which is centered again around the number 9, as each new value is 9 higher than the previous one, as follows:

Observations: many prime numbers appear in this table (bold).[6] Also note the palindrome structure in each row (e.g. in the row of 1, you will see 19 and 91, 28 and 82, etc.).
The Dual Aspects of Primes
In the first section, I started with the visible whole numbers, like 5, 37, 49, etc. and then dove into their invisible aspects by reducting them to single digits. Thus, from the hyungsang I deducted their sungsang. By this method I was able to show the dual characteristics of whole numbers of the n/1 type. In this section we look at numbers, as it were, from their flip-side, what is called their reciprocal side. Allow me to explain what I mean by this and how it translates into Unification Thought terminology.
Let’s imagine there are 7 people in a room. Before I can know this, I need to count each person. Thus, when I conclude that 7 is the result, and even write it down, what happens in our conventional way of writing just “7” is that we most likely take a most fundamental fact totally for granted. The truly correct way of writing down our result, as a mathematical formula, really ought to be 7/1, or 7 divided by 1, or 7 over 1. Just to blurt out “seven” is missing this salient, relationship-centered aspect.
The 7 people in the room enjoy two types of relationships:
• the group as a whole impacts each individual (relationships of the many to the one); and
• each individual experiences him or herself as part of the group and contributes to the group as a whole (relationship of the one to the many).
In mathematics, the only relationship we see covered, if at all in mathematical dictionaries, is the 1/n type, which in mathematical circles is called the reciprocal (or multiplicative inverse, a term I do not use). I have been very surprised to see how most mathematical dictionaries (if they have an entry on reciprocals at all, as many do not) gloss over the topic and only briefly mention it in a short paragraph with an example like 1/125, without writing it out in decimals.
I am taking the mathematical definition of reciprocal a step further, as I find regular mathematics one-sided in this instance. Reciprocity implies a relationship and the relationship between “n” and “1,” when staying true to Unification Thought, must be established in these two “mirror” formulas: n/1 an 1/n[7]
Thus: when the number 7 is given (as 7/1) and thus made visible, its reciprocal (as 1/7) is not visible and thus remains invisible. The opposite is also true: when I am given the 1/7 value, which is 0.142857…[7], then the “regular” prime number from which it was derived (as 7/1) is made invisible and would need to be figured out.
Although number theorists do not consider this dual structure of individual numbers in light of Oriental thought, I think nevertheless it is quite the correct way of doing so, and sets the tone and stage for our further investigations into the dual characteristics of numbers. The reason I am limiting myself to primes (a number that cannot be divided any further, like 3, 5, 7, 11, 13, etc.) should be obvious: they are the fundamental building blocks of numbers, as all other whole numbers are composites. Thus, there are two approaches: from the many to the one (as in 123/1) and from the one to the many (as in 1/123).
Visibility and invisibility in prime reciprocals
 The first prime number with an intriguing visible hyungsang and invisible sungsang aspect in its reciprocal value is the number 7. The number 7 is perfect for demonstrating my findings. Its reciprocal value is simply 0.142857… How do we calculate it? The drawing below illustrates the process:
The first prime number with an intriguing visible hyungsang and invisible sungsang aspect in its reciprocal value is the number 7. The number 7 is perfect for demonstrating my findings. Its reciprocal value is simply 0.142857… How do we calculate it? The drawing below illustrates the process:
The outcome of 1/7 is 0.142857….Let’s do the same analysis here: 1-4-2-8-5-7-1-etc. provides the following numeric differences: +3; -2; +6, followed by the mirrors of -3; +2 and -6. When put into two halves: 1-4-2 added to 8-5-7 gives us 999 (this is always true: the second half of a prime reciprocal added to its first half always adds to a series of 9s).
Take a look at the circled numbers, the values subtracted in the calculation: when added together in the correct 1/10th digit offset way[8], their sum is 0.999999…, which, rounded off, brings us back to 1.000….
The series of these values: 7-28-14-56-35-49-7, etc., can also be seen from the perspective of being either odd (O) or even (E) and then becomes: O-E-E-E-O-O, a mirror when divided into two halves of O-E-E and E-O-O. When we look at the numeric differences between these conse¬cutive values: +21; -14; +42; we see that they are followed by their opposites/ mirrors: -21; +14; -42.
A yang/yin type pattern also exists between the values that were left over after each subtraction, namely: 30-20-60-40-50-10-30…; the differences between them being: -10, +40, -20, followed by their opposites/ mirrors: +10, -40 and +20.
Also, if I take the non-circled numbers from each of which is being deducted, namely 1(0), 3(0), 2(0), 6(0), 4(0), 5(0), and we split this series in half, we have: 1-3-2 and 6-4-5, representing 1 through 6, and added together as two halves becomes 7-7-7 (132 + 645 = 777).
Dual characteristics hiding in prime number reciprocals
Let’s return to my handwritten calculation above once more. The solution to 1/7 = 142857…. Keep in mind that the number of repeat digits of a prime number reciprocal always follows the formula of n – 1. Thus, the number 7 has 6 digits in its reciprocal repeat section. The prime number 17 therefore would have 16 digits in one repeat section of its reciprocal (1/17 = 0.0588235294117647…; the starting zero is indeed also counted as one of the digits).
An inherent flaw?
We saw that the reciprocal value of 0.142857… seems to have a flaw: why is the 57 not a 56, as it would then more logically be the double of 28, which in turn is the double of 14? Let’s assume for a moment that the value is not 57, but indeed 56. And let’s also continue to assume that the doubling continues, but that for some mysterious reason we don’t see it (yet).
As before, we need to keep one rule in mind: 14, 28, and 56 all have just two digits, while the doubled values that follow after it start with three digits and will grow to many more, so I cannot just write 14-28-56-112-224-etc. as one continuous value (hyphens added). After all, what we get to see is only 0.1427857… and don’t visibly see any values over 57. If they are part of it, they must be very hidden.
The seemingly enormous problem of uncovering it is actually very easily resolved, if I adhere to a simple rule: I cannot make an illegal move and break the rule of only a two-digit advancement to the right. 14-28-57 are values that are two digits to the right of the previous value (14 is to be actually written as 0.14; 28 as 0.0028, and 57 as 0.000057, etc.)!
This is most important, and forces me to create some kind of overlap of digits. This is best illustrated in a table, where each new value is indeed two spaces to the right, and where we see that some digits come “underneath” a previous value; hence the overlap, but keep in mind that this analysis is still in the stage of dissection (zeros added for clarity):
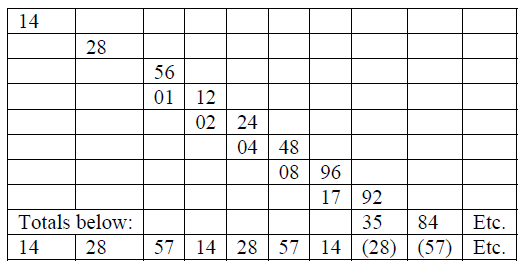
Thus, it is precisely because of these carefully considered and placed overlaps that the value of 142857…indeed appears in the reducted tables! What’s fascinating here is that apart from the fixed visible reciprocal of 142857… and the eternally growing invisible values of 14-28-56-112-224-etc. underneath it, which is its most fundamental structure, we also simultaneously witness a different kind of pair system and dual characteristic.
I will call the (largely; we only see the very beginning) invisible multiplication table of 14-28-56-112-224-448-etc. the sungsang of the prime number reciprocal. We do not really get to see it; but it is really there, hiding invisibly underneath it, but this sungsang is the very raison d'être, the very foundation and basis for the visible manifestation of it, what I would call the hyungsang of the reciprocal. The sungsang and hyungsang cannot exist without each other. The invisible is made visible, and its visible form cannot come about without the invisible. There are actually several other methods to construct the reciprocal of 7, and they all follow the same rule of hidden and revealed manifestations. I will show one later on.
Thus the simple looking 142857, and thus any prime number reciprocal for that matter, represents a far greater hidden reality. Please pay attention how I carefully word this; and you may have to read this definition more than once to grasp its meaning and implication fully:
The visible numerical value of a prime number reciprocal not only hides the internal hidden invisible structure, but is also its only possible visible manifestation. The invisible aspect is its root, its very foundation. The two aspects belong together and thus form a pair, one is visible, the other is (largely or completely) invisible.
Subject and object in Unification Thought
It may be safely assumed that the invisible sungsang of a prime number reciprocal stands in the subject position, following Unification Thought, as the fundamental multiplication series is primary, and that the hyungsang aspect, its visible manifestation, stands in the object position, because there is clear cause and effect.
Likewise, it may be safe to assume that the sungsang aspect of whole numbers in their reducted form (e.g. 5 as a form of 14) stand in the subject position, and that the whole numbers, which are their non-reducted outer manifestations, stand in the object position. Probably we can also assume cause and effect here.
However, it is impossible to designate the plus values in the yang-yin type numeric differences as subject or the minus differences as object; after all, the plus or minus results totally depend whether you move from left to right, or from right to left, as both directions are possible, even though we only followed the Western convention of writing from left to right.
Even the multiplication tables of prime number reciprocals as such can be read as division tables from right to left as well! This is especially beautifully displayed in the reciprocal of the prime 19, as 1/19 = 0.052631578947368421…, where from left to right the hidden sungsang series is actually based on 5-25-125 (or, more precisely put: 51, 52, 53, etc.) and from right to left you see you see the series of 1-2-4-8-16 (based on 20, 21, 22, 23, 24, etc.), which is a multiplication table running in the opposite direction from right to left! But it is obviously a division table at the same time, when viewed from the left to right direction.
Due to overlap, both divisions and multiplications soon become invisible. The “out of blue” appearance is thus an illusion, based on a very precise and absolute sungsang pattern. That two multiplication series can run simultaneously in opposite directions is nothing if not mind boggling to watch. In very large prime number reciprocals I have even witnessed tables within tables, i.e., all kinds of multiplication series sprout up all over the place in the reciprocal, only to disappear again due to overlap. The digits seem at once totally random, but are nevertheless totally orderly. Allow me to give you one small example. In the prime number reciprocal 1/83 = 0.01204819277108433734939759036144578313253…, in the bolded section 9-036-144-578 (hyphens added), we discover a second multiplication series, as 9 x 4 = 36, 36 x 4 = 144, etc.
Are there any yang-yin patterns in the sungsang aspect of prime number reciprocals, one might ask? Yes, there are, but again, the only way to see them is by reducting the values involved. Here follows thus another basic definition, which we already saw above: all multiplication tables, when reducted, reveal perfect plus/minus, yang-yin patterns, as well as many palindrome mirrors.
Thus, without the fundamental basis of the invisible sungsang, the yang and yin could never become manifest. In Unification Thought it is stated that all attributes of dual characteristics are totally One within God but are outwardly manifested in Creation. The same holds true for numbers: the invisible possesses all the inherent attributes that can be discerned as existing outwardly. This is a most mysterious thing to watch: I keep asking myself; how can a simple multiplication series give birth to so many mirrors, palindromes, absolute patterns, yang-yin patterns, and many more aspects which I have no space for to cover here? And yet, that’s the way it just is. To paraphrase what God told Moses: Numbers are what they are.
Two types of reduction or overlap
The hyungsang of a prime number reciprocal is also a form of reduction of its sungsang original: after all, we apply the rule of not allowing progressive placement to the right to be more than the number of digits of the starting number, which we saw demonstrated above when we dealt with the reciprocal of 7. Thus, in a table of columns and rows, we see how digits from consecutive rows are placed in the same column and will be added together, by the process of reduction, as all addition is a form of reduction.[9]
Let me give another example, by introducing the following series: 1-3-9-27-81-243-729… based on x3 multiplication, which can be mathematically indicated by the formula of: 30, 31, 32, 33, 34, 35, etc. I have to place them properly in a table:

We have thus found another way to construct the reciprocal of the number 7, and there are more ways to do so! Since the digits of values have to be placed underneath digits in the rows above, which I have called a process of overlapping, I am in fact practicing a process of reduction on a vertical level. In Column E, for example, I am reducting four digits of rows EE through HH.
Thus, I can take any whole number, put it properly into a multiplication table with rows and columns, by following the formula of n0, n1, n2, n3, n4, n5, etc., with the proper decimal offset factors included, and end up with a prime number reciprocal! And the hyungsang value of the reciprocal can only become visible via the process result of overlapping and reduction of the sungsang values.
As we saw how with the number 3 we constructed the reciprocal of 7, there is also a decimal factor involved, as 10 – 3 = 7. Likewise, I can construct the reciprocal of 19 by starting a multiplication series based on 810, 811, 822, etc., as 100 - 81 = 19. Or I can do it vice versa.
What we just saw above actually mirrors perfectly with what we find with whole numbers, already discussed in the first section. We know that any reduction can represent a basically infinite series of original whole numbers, as e.g. 1, 19, 28, 37, but also 9485763859375937589346 reducts to 1. Other numbers reduct to 2 through 9. Any number larger than 9, no matter how large, in its reducted form, belongs to a value between 1 and 9.
The reduction process of whole numbers, like 12345, can be approached, in light of the decimal offset we saw in above, with the very simple process of addition, from a different perspective. The method of 1 + 2 + 3 + 4 + 5 = 15 = 1 + 5 = 6 is child’s play. We should approach it also from the overlap-based reduction process.
First, I break 12345 down into 10000, 2000, 300, 40 and 5. In prime number reciprocal tables I carefully moved one step or more steps to the right with each new value. In this case, as I am working in mirrors I need to move each last value to the left. Remember how in the table of the reciprocal of 7, I placed a zero in front of 112, as 0112 for clarity, and I have to do the same thing, in reverse, for the number 12345. Thus, I first place a zero behind the 5 and turn it into a 50 and then place it underneath the 40 to add to 90. I then add a zero to this new subtotal 90 to become 900 and add it to 300 to become 1200. Next I turn 1200 into 12000 and add it to 2000 to become 14000, and then turn it into 140000 to add to 10000 to become my semi-final result of 150000; I can then repeat the entire process in just two steps and turn 50000 into 500000 and add it to 100000 to become 600000, after which I discard the zeroes to become the simple 6 we already established earlier.
Needless to say, I can also do the entire process in reverse: turn the 10000 to 1000, add it to 2000, to get 3000; then turn it into 300; add it to 300 to make 600; turn or reduce it into 70 and add it to 40 to make 100. Then reduce the 100 to 10 and add 5 to make 15, and 1 + 5 = 6.
An approach from the left or right is equally valid and gives the same end result. Of course, we will stick to the easy method, but we need to know what is really involved. Thus we see that there are parallels between the world of whole numbers (primes) and the world of their reciprocals, that they mirror each other very well, they reiterate Unification Thought’s notion of the two types of dual characteristics.
Thus, we see once again that considering the 1/n and n/1 approach as two sides of one reality is the correct way to approach numbers.
Having Fun with Numbers
I order to solidify and help you do your own research, I am going to provide a few more examples of how yang-yin structures show up when I start “playing around” with prime number reciprocal values. At this point, little commentary will suffice.
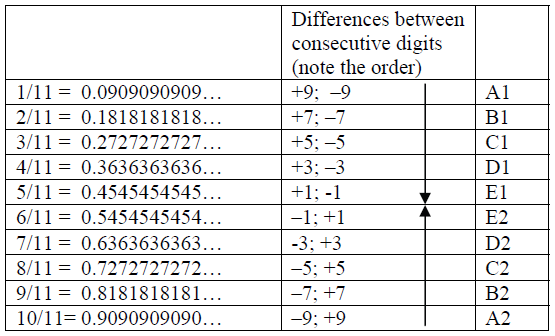
Note that the total of each mirror pair, like B1 and B2 is always 11/11 or 0.9999999999… = 1.0000…. The vertical arrows show an overall mirror as well. There is a descending order of odd numbers (9-7-5-3-1), followed by an ascending order, and notice the yang-yin and mirror correlation between A1 and A2, B1 and B2, etc.
My second challenge to you is a simple one: figure out, from what you have learned here, why the reciprocal of 81 contains a continuous reciprocal repeat of (0.)012345679… where the 8 is missing for some mysterious reason. What is the real series, or sungsang, hiding underneath this hyungsang appearance? Considering that the universe is composed of just 81 stable chemical elements, this puzzle is worth unraveling.
My third game, actually more of a puzzle: find the Fibonacci series and then make a table where the digit advance to the right is only one, since the very first digit of this series has only one digit, and you will find a number that is the reciprocal of the number 89.
My final game is to show you some of the pervasive nature of prime number reciprocal series, as well as the yang-yin balances, by showing what happens with a somewhat unusual approach: I reduce the digits of 1/7, which is 0.142857…first to its first digit, then it expand it to two digits, then three, etc., and multiply them with a random number (you can try this approach with a different factor and see what you will get):

Study to see what you get if you did things the other way around: focus on the last digit of 142857 and then expand to two digits, etc., and then multiply by 7; and thus: first 7 x 7, then 57 x 7, followed by 857 x 7, then 2857 x 7, and continue for a while. You will discover some amazing results, and a total of +10 and -10 in the numeric differences between, this time, the first digits of the results. Also, see what happens with these calculations: 1/7, 2/7, 3/7, etc. The perfect and especially absolute nature of the prime number 7 will become even more apparent to you!
Many more “games” are possible and I invite my readers to start “playing” with these numbers as you wish.
Final Observations
What can we conclude from this rather brief introduction into the fascinating world of the two types of dual characteristics found in prime numbers?
- As prime numbers are the fundamental building blocks of all numbers, our study has to start with them.
- Prime numbers have two aspects that need to be studied as n/1 and also as 1/n, that is, from a relational, or reciprocal perspective. Thus prime numbers are like coins with two mirror sides. We study from the many to the one, as well as from the one to the many. I treat them as two sides of one reality. They are mirrors of each other.
- Basic math consists of multiplication tables. These tables can be studied from two perspectives: their outward visible values, their hyungsang, and via the process of reduction, we discover their inner core or sungsang values.
- In the reducted tables of whole numbers, we discover the first evidence of yang-yin type mirrors in their numeric differences.
- When moving to the 1/n aspect of a prime, or its reciprocal as it is called in mathematics, we discover perfect yang-yin mirrors in the calculation process (values taken out and values left over), as well as in the final result of such calculations, when analyzed from the perspective of numeric differences.
- Furthermore, we also discover in the prime number reciprocal a hidden structure, which is the foundation for the visible value. This hidden multiplication series, in light of Unification Thought, I have called the sungsang, and the outward visible appearance, and the result of the 1/n calculation, its hyungsang.
- The sungsang and hyungsang are co-dependent: the sungsang cannot express itself without the hyungsang, and the hyungsang cannot exist or be expressed without the sungsang. The invisible and the visible are two sides of one reality.
- The sungsang is the subject, while the hyungsang is its object.
- We also discovered that the process of reduction is present in the sungsang structure becoming its visible hyungsang expression, in prime number reciprocals, caused by the inevitable overlaps.
- Reduction and overlap are already a normal part of mathematics: we see it daily in the two-directional activity of addition and subtraction, as well as in two-directional multiplication and division. Thus in every day counting, we are constantly faced with invisible structures and visible results.
- Even though the written form of a number can only be two-dimensional, in palindromes we discover left-right directionality, and in palindrome tables we additionally see up-down.
- Palindromes are perfect examples of yang-yin type of dual characteristics.
- We have witnessed the pervasive centrality of the number 9.
Personally, I find only confirmation and no conflict between my findings and Rev. Moon’s delineation of the two types of dual characteristics: sungsang and hyungsang as well as yang and yin. In actuality, for me, it was exactly because of these dual types of distinctions in Unification Thought that I not only started to see a consistent pattern, but also found it the only possible and correct interpretative model to make sense out of the literally more than a thousand pages of notes I had produced during my initial very enthusiastic, but yet unfocused research.
If indeed Unification Thought is true, then evidence of it in all sorts of academic endeavors will eventually be found. As far as my research into the world of numbers is concerned, which also includes a mathematical model of the Unification logo[10] (which is based on prime numbers), among many other discussions, all I can say is this: So far, so good. Thanks to Rev. Moon, I have been graced by being able to add a new dimension to mathematics.
Notes
[1] Journal of Unification Studies 8 (2007):125-137.
[2] In the West, often the expression “Yin and Yang” is used in that order, but in all oriental writing, the order is always Yang-Yin, and since this paper deals with Oriental and Unification Thoughts, I have opted to maintain the traditional order.
[3] See Adrian de Groot, Number Theory in Light of Unification Thought: Preliminary Findings (Tokyo: Unification Thought Institute, 2005); Richard Heath, The Matrix of Creation (St. Dogmaels: Bluestone Press, 2002); Robin Heath, Sun, Moon, & Earth (New York: Walker & Company/Wooden Books, 1999); and especially John Martineau, A Little Book of Coincidence (New York: Walker & Company/Wooden Books, 2001).
[4] The “zero” is a digit, invented in India, and represents a clever way to help us deal with the next repeat of 1 through 9, by adding a zero to the 1, making it 10. Thus 10, 20, etc. indicate the 2nd and 3rd, etc. repeat of a fundamental series, namely in this case 1 – 9. Thus, we need to keep in mind what modern writing conventions are fundamentally all about. One could argue that the decimal system is from 0-9, while most believe it is from 1-10.
[5] Keep in mind that all additions are already a common form of reduction: when, for example, I add 35 to 29, I carry over the 10 of the first total of 14, over to the next column to the left (and we ordinarily ignore the 0), so that the 30 + 20 elements do not total to 50 but to 60, as the total is 64. In reverse, subtraction is also a form of reduction. A beautiful example of inherent, but not expressed and yet often partially visible, reduction can be seen in the table of 11. It goes simply first from 11 to 22, then 33, 44, etc., and after 99 we have values like 110 (add the first one to the end, and you have 11 once again), then at some point 143 (which you can easily see is the expanded, exploded form of 44), etc. In other words: the inherent 11-based foundation remains quite discernible.
[6] See Adrian de Groot, The Secret World of Numbers, self-published and available from www.numbersecrets.net or www.lulu.com, on why the squared primes like 25, 49, etc., can also be considered to be prime.
[7] The three dots after the numeric digits indicate that these digits, after the decimal point, keep repeating themselves into infinity. Thus 1/7 = 0.142857142857142857142857-etc. The other convention is to place a line over the digits.
[8] That is: 0.07 + 0.028 + 0.0014 + 0.00056 + 0.000035 + 0.0000049 + etc. = 0.9999999… = 1.000….
[9] See note 5
[10] See Peter Plichta, God’s Secret Formula: Deciphering the Riddle of the Universe and the Prime Number Code (Rockport, MA: Element Books, 1997); and de Groot, Number Theory in Light of Unification Thought.
